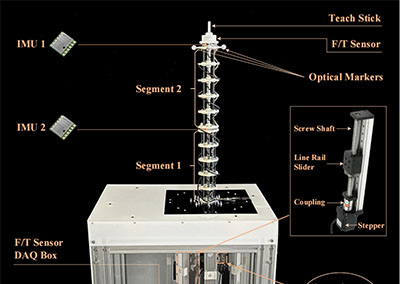
多机器人的运动规划是个有挑战性的课题。众多机器人同处于同一个空间，要在运动学和编队约束条件下，实现高效计算，实现多机器人到达目的地，并避免相互碰撞。
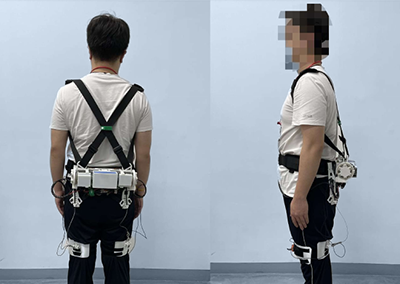
来自哈尔滨工业大学的研究团队提出了一种新颖的集中式轨迹生成方法，并利用NOKOV度量动作捕捉系统在真实实验中验证了算法的效率、适应性和可扩展性。论文被IROS2021收录。
论文检索页
算法原理
多机器人运动规划方法可以分为两大类：
分布式方法通过邻近机器人之间的局部交互来实现群体行为，对通信的要求低、可扩展性强。然而很难在个体或系统层面施加约束。
相比之下，集中式方法能提供全局保证，并能合理地设置约束条件，但随着机器人数量的增加，它们的扩展性往往很差。
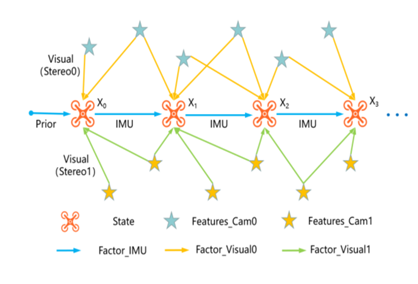
研究团队将著名的运动规划方法GPMP2扩展到多机器人场景，采用稀疏高斯过程模型，高效地计算多机器人运动轨迹。
通过添加队形约束条件，多机器人编队可以自适应地通过不断变化的地形。并提出一种增量重规划算法，使用贝叶斯树的数据结构来更新运动轨迹，实现快速的在线操作。
实验过程
研究团队用一组四旋翼飞行器测试了算法框架。
实验在三种常见场景中进行，分别是：保持队形、为改变目的地重新规划，以及在宽度变化的空间中通过时自适应变换队形。
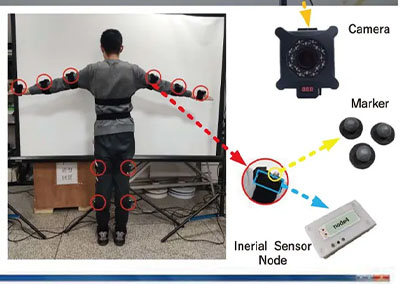
一组Crazyflie纳米四旋翼飞行器在NOKOV动作捕捉系统的监控下进行了实验。飞行器通过CrazyRadio PA接收来自NOKOV动作捕捉系统的信息，以进行定位。
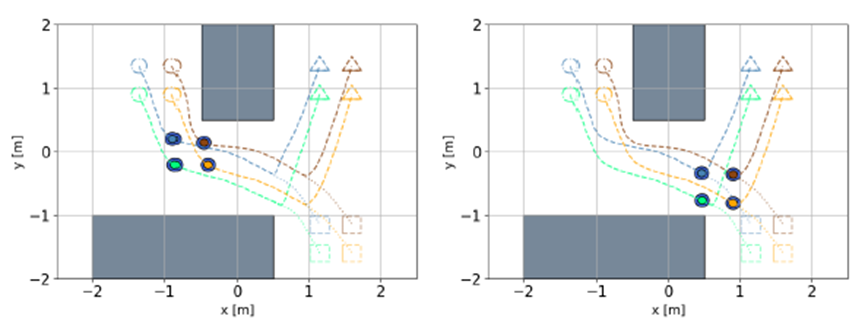
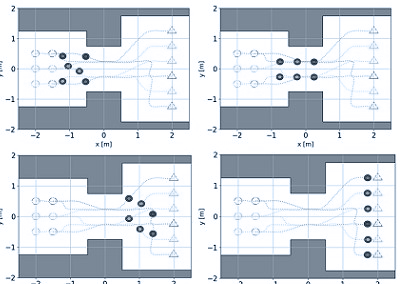
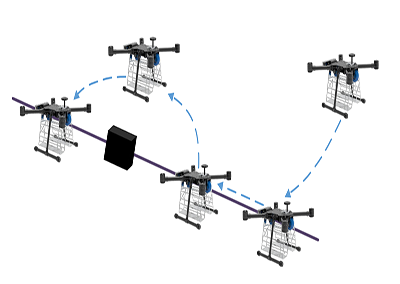
实验1+实验2运行轨迹，2.4、7.0秒快照。原目标标记为正方形，新目标为三角形
实验1+实验2：保持队形、改变目的地重新规划在实验1中，4架四旋翼机保持方形队形飞向目标，同时避开障碍物。四旋翼机编队在必要时会做出取舍，编队在转弯时有轻微的扭曲，但可以实现更平稳的转弯。
在实验2中，四旋翼机编队飞向原始目标途中，突然改变目标点。在t = 7s时将目标点向与原始目标相反的方向移动。增量重规划算法在4ms内将轨迹更新到新目标，满足实时性要求。
实验3：在宽度变化的空间中自适应变换队形6架四旋翼机在2.5m、1.5m、3.5m三种不同宽度的空间中通过。全局规划算法计算出的不同队形和执行时间间隔为：(i) 1s−2s: 3×2排列；(ii) 4s−7s: 2×3排列(iii) 9s−10s: 6×1排列。
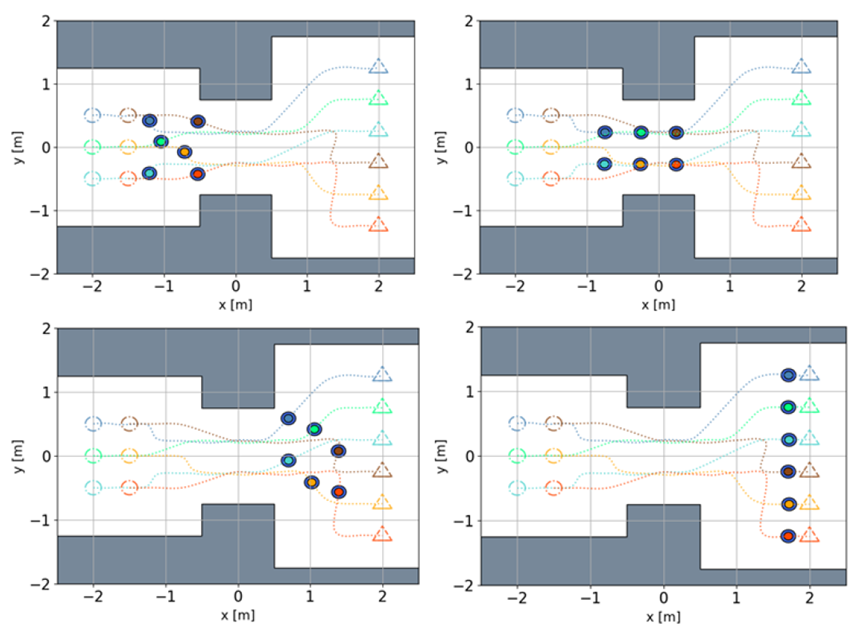
6架四旋翼机变换队形，2.4秒、4.0秒、7.4秒和9.0秒快照
此外，在四重地图上实现了10架四旋翼机通过宽度分别为:4m、2m、7m的空间。对应的编队配置为:(i) 1s−2s: 5 ×2;(ii) 4s−7s: 2 ×5;(iii) 9s−10s: 10 ×1。
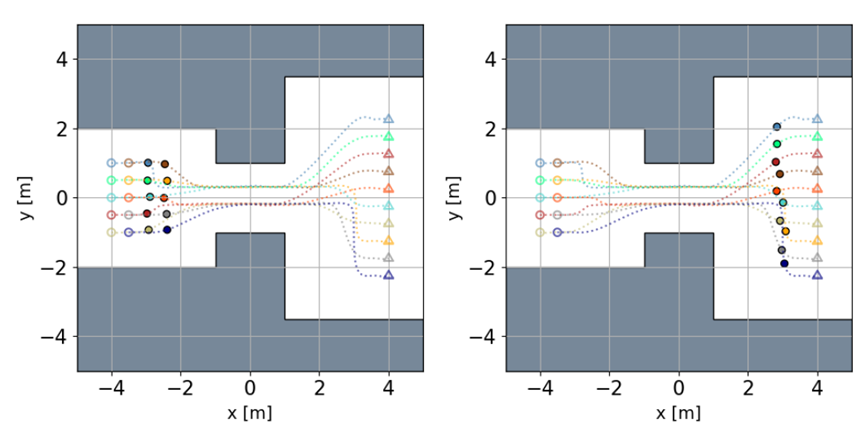
10架四旋翼机变换队形，2.0秒和8.0秒快照
算法运行时间
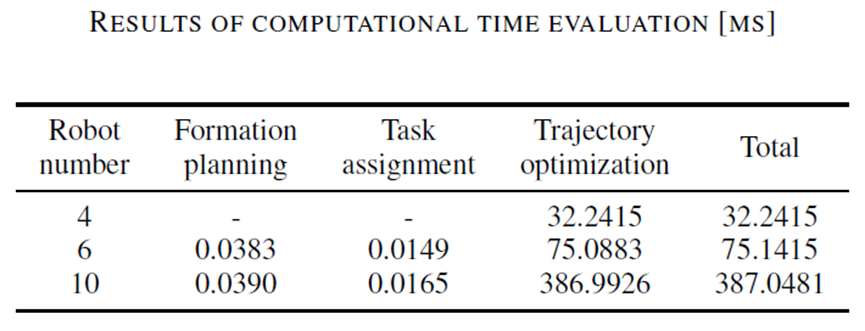
算法运行时间
该算法能在 0.39 秒内计算出 10 架四旋翼机的完整轨迹，并能进行编队变化，这对于如此复杂的任务来说是非常高效的。
参考文献：
更多详情，请留言
-
您可致电010-64922321或在右侧留言，获取您专属的动作捕捉解决方案与报价单
-
- 领域 *
- 提交留言
